FIR滤波器与IIR滤波器的区别和比较

IIR 滤波器和FIR 滤波器的比较和区别

1. 两种滤波器都是数字滤波器。根据冲激响应的不同，数字滤波器分为有限冲激响应（FIR）滤波器和无限冲激响应（IIR）滤波器。对于FIR 滤波器，脉冲响应在有限时间内衰减为零，其输出仅取决于当前和过去的输入信号值。对于IIR滤波器来说，脉冲响应理论上应该是无限期的，它的输出不仅取决于当前和过去输入信号的值，还取决于过去信号的输出值。 

2. FIR：有限脉冲响应滤波器。有限意味着您的脉冲响应是有限的。与IIR相比，它具有线性相位和易于设计的优点。这也说明IIR滤波器具有非线性相位的缺点，不易设计。另一方面，IIR有一个FIR没有的缺点，即要设计一个参数相同的滤波器，FIR需要比IIR更多的参数。这也说明应该增加DSP计算的次数。 DSP 需要更长的时间来计算，这会影响DSP 的实时性能。以下都是低通滤波器设计。 FIR设计：FIR滤波器的设计比较简单，就是设计一个近似理想低通滤波器的数字滤波器。通常，这种理想的低通滤波器是频域中的矩形窗口。根据傅里叶变换，我们可以知道这个函数是一个时域的采样函数。通常这个函数的表达式是：sa(n)=sin(n)/n，但是这个采样序列是无限的，计算机无法计算。因此，我们必须削减这个采样函数。也就是加个窗函数。这就是传说中的窗户。即，为了将这个时域采样序列乘以一个窗函数，这个无限的时域采样序列被截断为有限数量的序列值。但是，加窗后，采样序列的频域也有影响：此时的频域不再是理想的矩形窗口，而是具有过渡带和阻带波动的低通滤波器。通常，根据所加窗函数的不同，对采样信号进行加窗后，在频域得到的低通滤波器消隐带的衰减也不同。我们一般根据这个阻带衰减选择一个合适的窗函数。如矩形窗、汉宁窗、汉明窗、BLACKMAN窗、凯撒窗等。选择特定的窗函数后，根据设计的滤波器的参数，计算出所需的窗函数阶数和表达式。然后用这个窗函数乘以采样序列，得到实际滤波器的脉冲响应。 IIR设计（双线性变换法）：IIR的设计理念是这样的：根据要设计的滤波器的参数确定一个模拟滤波器的传递函数，然后根据这个传递函数，通过双线性变换，或者脉冲的采用不变响应法设计数字滤波器。其设计较为复杂，其复杂性在于确定其模拟滤波器传递函数H(s)。我们可以让软件做到这一点。然后说一下你的具体实现步骤——你需要先确定你需要什么类型的滤波器，巴特沃斯型，切比雪夫型，或者其他类型的滤波器。

选择模型后，可以根据设计参数和滤波器计算公式确定传递函数的阶数和表达式。通常在这个过程中存在预失真问题（这只是双线性变换方法中需要注意的问题，不变脉冲响应方法没有这个问题）。确定H(S)后，可以通过双线性变换得到数字域中的差分方程。 3.对于IIR和FIR的比较，有些书上有讨论。我引用了陈怀臣的《数字信号处理教程-MATLAB的解释与实现》：在性能上，IIR滤波器传递函数包括两组可调因子，零和极点，唯一的极点限制在单位圆内。因此，可以使用较低的阶数来获得高选择性，使用的存储单元数量少，计算量小，效率高。但是这种高效率是以相位非线性为代价的。选择性越好，相位非线性越严重。 FIR滤波器传递函数的极点固定在原点，不能移动，只能通过改变零点的位置来改变其性能。

因此，要实现高选择性，必须使用更高的阶数；对于相同的滤波器设计指标，FIR滤波器所需阶数可以是IIR滤波器阶数的510倍。因此成本较高，信号延迟也比较大；如果需要线性相位，IIR滤波器必须增加一个全通网络进行相位校正，这也大大增加了滤波器的阶数和复杂度。 FIR 滤波器可以具有严格的线性相位。从结构上看，IIR滤波器必须采用递归结构来配置极点，保证极点位于单位圆内。由于有限字长的影响，计算过程中系数会四舍五入，造成极移。这种情况有时会导致稳定性问题甚至寄生振荡。相反，只要FIR滤波器采用非递归结构，理论上或在有限精度的实际运算中都不存在稳定性问题，因此引起的频率特性误差也很小。此外，FIR 滤波器可以使用快速傅立叶变换算法，并且在相同的顺序下计算速度可以快得多。对高稳定的晶体振荡器（高稳晶振）和高功率小型化腔体滤波器和介质滤波器都有成倍的配套需求，对其指标要求也很高；对应基站配套需求的时钟模块产品、授时守时模块和时频模块对应的同比例的需求情况。

另外，还需要注意的是，IIR滤波器的设计虽然简单，但主要用于设计低通、高通、带通、带阻等分段特性恒定的滤波器，往往与模拟滤波器模式。 FIR滤波器灵活得多，尤其容易适应一些特殊的应用，如构成数字微分器或希尔伯特变换器等，因此具有更大的适应性和广泛的应用领域。从上面的简单对比可以看出，IIR和FIR滤波器分别有所长，所以在实际应用中需要从多方面考虑选择。从使用需求来看，IIR最适合于对相位要求不敏感的场合，比如语言交流，让您可以充分发挥其性价比的特点；用于图像信号处理、数据传输等系统。在波形中携带信息。线性相位要求更高。如果可能，最好使用FIR 滤波器。当然，在实际应用中可能需要考虑更多的因素。不管IIR和FIR，阶数越高，信号延迟越长；同时，在IIR滤波器中，阶数越高，对系数的精度要求越高；否则，极点移出单位圆时容易造成有限字长误差。因此，在顺序的选择上要充分考虑。 IIR滤波器（切比雪夫滤波器） 滤波器比较（IIR和FIR，数字和模拟）第19、20、21章，主要讲IIR滤波器和滤波器的比较IIR滤波器没有使用卷积运算，而使用递归运算（递归），所以执行速度很快，但性能不一定比FIR滤波好。 IIR 的脉冲响应由衰减的指数信号组成。 IIR进出的重复率是：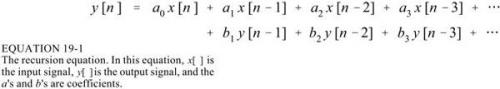

IIR的递归系数与其频率响应的关系可以通过Z变换进行变换，这里不涉及。通过取不同的递归系数（下图中的a和b），可以实现不同的滤波器：（9501.163.com）

当然，这是最简单的应用。递归系数的选取有一些细节和公式，这里不再赘述。 FIR 可以是线性相位，即脉冲响应是对称的，而IIR 通常是非线性相位。这是因为FIR 在设计过程中决定了时域和频率响应中的波形，而IIR 决定了设计中的递归系数，无法确定您的波形是什么样的。 

IIR实现线性相位，可以进行双向操作，如下图：（9504.163.com）

切比雪夫滤波器切比雪夫滤波器（Chebyshev）应用于频域，其性能当然无法与同步窗函数滤波器相比，但速度非常快。 Chebyshev 响应是一种数学策略，通过允许频率响应中的纹波来实现更快的衰减。随着波纹度增加（坏），下降变得更剧烈（好）。 

了解极点：极点越多，性能越好。滤波器系数可参照下表确定。各种滤波器的比较1. 模拟与数字如果信号需要过滤，是否在模拟相位上过滤？还是数字化后过滤？下图做一个对比，可以看出数字滤波器的性能与模拟滤波器难以实现，但速度较慢，模拟滤波器的幅度和频率具有更高的动态范围。 

本例中模拟滤波的实现：

2、sinc vs Chebyshev窗函数对比下图（9508.163.com）

sinc窗函数使用卷积进行运算，而Chebyshev使用递归方程。当然，卷积可以用fft卷积来完成，即先DFT，再进行频域的4个算术运算，再进行逆DFT变换。这可以提高速度，但仍然不如递归方程快。另一方面，同步窗函数的滤波性能可以很好的发挥。 

3. 移动平均对极点

[声明]文章版权归原作者所有，内容为作者个人观点，本站只提供参考并不构成任何投资及应用建议，转载目的在于传递更多信息，并不代表本站赞同其观点和对其真实性负责。如涉及作品内容、版权和其它问题，请在30日内与本网联系，我们将在第一时间删除内容！